ジグソーモデルは中野先生が提案された,ジグソーパズルを利用したメタモルフィズムの計算機構,です.
計算の途中の状態をジグソーパズルのピースに見立て,入力と時々の状態に対してうまく当てはまるようにピースを並べていけば計算が終わるという楽しい計算機構です.データの与えられ方によっては並列に計算できたり,入力が中途半端に与えられた状態でもできる部分から計算できたり,という特徴があります.
2013年のプログラミングシンポジウムで話を聞いたときに,HDLで書いてハードウェア化してみるのもいいかなーと思いながらも,なんとなく2016年の今日までそのままに…
とりあえずは最初の例題くらいは実装しておこうと,ふと試してみました.
計算の仕組みの詳細は,日本語で記述された論文として,2013年のプログラミングシンポジウムがダウンロードできるので,原稿を読むとよいでしょう.
Synthesijer.Scalaを使って実装してみたコードはこちら.
といっても,実装する上で難しいことはしていなくて,右と上の状態を元に左としたの状態を決定して,伝播させるというもの.規模は,回路生成時に静的に決めることにしています.とりあえず,ピースをFFで持つ回路(mkJigsaw3to2_FF)と,組み合わせ回路(mkJigsaw3to2_Expr)を考えてみています.
mkJigsaw3to2_FFとmkJigsaw3to2_Exprのシミュレーション結果はこんな感じ./も%もなしで201(3)が10011(2)に変換できていることがわかります.ピースをFFで実装した版は徐々に値が確定している様子がみてとれますし,FF使ってない版は1クロックで値が確定しますね.
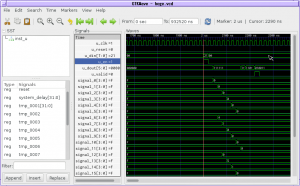
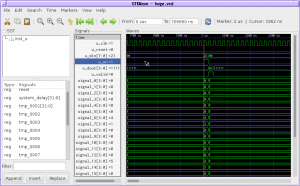
仮に7シリーズを対象に合成してみても,入力が4桁の3進数,出力が6桁の2進数という程度の規模なら,どちらも300MHz越えくらいの動作周波数で動きそう.
もっとも,大きな規模になると組み合わせ回路では遅延が厳しく,ピースを全部FFに置くのもリソース的に厳しいでしょう.ピースをブロックメモリとか外部メモリに置いて適当に処理を分割する必要がありそうだな,ということは容易に想像がつきます.といいますか,それを考え出し始めるあたりからが本番という気がします.
さて,なにか面白い応用例ないかな.
ちなみに,検索してみたところ,西尾さんが2013年当時に,ジグソーパズルで素数を生成するというのをされている.今度実装してみようかな.