GoogleのTPU論文で界隈が賑わっていますが,いくつか目をひくポイントの一つが256×256のシストリックアレイな行列演算器ではないでしょうか.
というわけで(?)シストリックアレイな行列演算器をSynthesijer.Scalaで書いてみました.
ソースコードは mkSystolicMatrixMultiplicationUnit.scala です.
FPGAの原理と構成によると,シストリックアレイは,
単純な演算を行う多数の計算要素(PE)を規則正しく配置したもの
で
各PEの演算とデータ授受によりアレイ内をデータが流れるこのような動作は,あたかも心臓の律動的な収縮(Systolic)により血液が流れる様子のごとく捉えられることから,シストリックアレイとの名前が付けられている.
だそうです.
まずは,シストリックアレイのPEとして,行列積の各要素の答えを求めるMAC演算器を作ります.コードは次のように感じ.
class mkSystolicMatrixMultiplicationCell(w:Int)
extends Module("systolic_mmu_pe_"+w, "clk", "reset"){
val ain = inP("inA", w); val ain_valid = inP("inA_valid")
val bin = inP("inB", w); val bin_valid = inP("inB_valid")
val aout = outP("outA", w); val aout_valid = outP("outA_valid")
val bout = outP("outB", w); val bout_valid = outP("outB_valid")
val cout = outP("outC", 2*w)
aout $ sysClk := ain // 入力aを1クロック後に出力aに
bout $ sysClk := bin // 入力bを1クロック後に出力bに
aout_valid $ sysClk := ain_valid
bout_valid $ sysClk := bin_valid
val c = signal(2*w); cout := c // 結果格納レジスタを用意.coutに接続
val ab = signal(2*w); ab := ain * bin
// リセットで0クリア,入力が有効ならMAC演算を実行,無効ならそのまま
c $ sysClk := ?(sysReset == HIGH, value(0, 2*w),
?((ain_valid and bin_valid) == HIGH, c + ab,
c))
}入力データのain,binを1クロック後にaout,boutに出力するとともに,内部レジスタcをain*bin+cで更新するという単純な回路ですね.
シストリックアレイ化するには”多数の計算要素(PE)を規則正しく配置する”とよいのですが,今回は二次元に配置することにします.配置するコードはこんな感じ
val cell = new mkSystolicMatrixMultiplicationCell(w)
val PEs = for(i <- 0 until n*n) yield instance(cell, "U_"+i)
for(r <- 0 until n){
for(c <- 0 until n){
val i = r*n+c
// horizontal connections
if(c == 0){ // from input
PEs(i).signalFor(cell.ain) := a_inputs(r)
PEs(i).signalFor(cell.ain_valid) := a_valids(r)
}else{ // from the above cell
PEs(i).signalFor(cell.ain) := PEs(i-1).signalFor(cell.aout)
PEs(i).signalFor(cell.ain_valid) := PEs(i-1).signalFor(cell.aout_valid)
}
// vertical connections
if(r == 0){ // from input
PEs(i).signalFor(cell.bin) := b_inputs(c)
PEs(i).signalFor(cell.bin_valid) := b_valids(c)
}else{ // from the left cell
PEs(i).signalFor(cell.bin) := PEs(i-n).signalFor(cell.bout)
PEs(i).signalFor(cell.bin_valid) := PEs(i-n).signalFor(cell.bout_valid)
}
c_outputs(i) := PEs(i).signalFor(cell.cout)
}
}1行目で定義しているcellは,シストリックアレイを構成する演算器のテンプレートで,実際のインスタンス生成は2行目です.4行4列ならば,n=4として16個のインスタンスが生成されることになります.
4行目以降の部分では,入力データを受け取る端の部分に注意しながら,各要素の入力と出力を接続しています.
入出力ポートを整理してモジュールとしての体裁を整え,テストベンチでシミュレーションすると,こんな感じで動作の様子が確認できます.
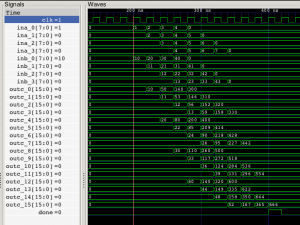
次々とデータが投入しはじめてから11クロック目にはすべての要素の計算結果が揃うことが確認できました.